Avrei necessità di congiungere tramite polilinea due punti tra i quali può esserci un ostacolo. La congiungente deve essere quella più breve possibile. Ad esempio. Immaginate una scatola di scarpe aperta superiormente e poggiata su un tavolo, dentro c’è una sferetta e fuori la scatola, sul tavolo ce c’è un’altra. Io devo unire i centri delle sferette tramite una polilinea che può anche toccare il bordo della scatola, ma non deve attraversarla.
Avete qualche idea o conoscete qualche plugin?
Questo caso sembra semplice, dato che il bordo della scatola ha altezza costante.
Disegni la congiungente i centri e poi ‘sollevi’ il punto che interseca la parete fino al bordo superiore …
O non ho capito il problema ?
Ciao Luca.
La mia idea è questa.
Ovviamente si deve fare riferimento a un piano.
ostacolo.gh (22,3 KB)
Hai capito benissimo.
Anche se ho capito … ripensandoci … ho dato la risposta sbagliata, scusa … ![]()
Quanto ti ho detto vale solo se la pareta della scatola e’ perpendicolare alla linea che congiunge le sferette.
Se no la cosa mi pare piu’ complicata …
Provo a cercare il modo … ma non prometto, sorry. ![]()
EDIT:
No, analiticamente non sono capace …
Penso che finirei col fare delle ricerche dicotomiche lungo i 4 lati della scatola …
Interessante, ma quando la sfera è all’interno della scatola non funziona. La polilinea deve “uscire” dall’apertura.
Prima graficamente, poi si vede la parte analitica.
A me viene in mente un fascio di piani che passano per la congiungente e intersecano l’ostacolo. Ci provo..
Forse così?
ostacolo a.gh (16,8 KB)
Ciao Filippo, potrebbe servire un _Project, della congiungente i due punti, sulla superficie delle scatole?
Non dovrebbe essere poi difficile evidenziare i punti di interesse per la spezzata “minima”.
O no? ![]()
[quote=“Gambler, post:9, topic:6740”]
potrebbe servire un _Project, della congiungente i due punti, sulla superficie delle scatole?
[/quote] Sì certo, ma se la congiungente giace sul medesimo piano della base? Inoltre, l’obiettivo e validare il modello anche in presenza di un semplice ostacolo frapposto e non necessariamente piano. Ma andiamo per gradi.
Intendi che i due punti (sfere) giacciano sullo stesso piano, sul fondo delle scatole?
Si, può capitare.
Come? Perché quel cilindro?
Il cilindro l’ho inserito perché mi hai parlato di altri elementi frapposti. ![]()
Fai come se non ci fosse.
Qui i due punti sono sul fondo della scatola.
Proiettando la congiungente i due punti (sfere) sulle superfici e unendo opportunamente mi pare ci sia tutto per tracciare la spezzata minima.
Non so usare GH, penso servano delle liste dove si prendono i valori massimi in Z delle intersezioni e si ragioni con la distanza dei vari punti dai due punti originali (sfere) per avere l’ordine con cui unire i vertici della spezzata.
Scusa Fabio, intendi proiezione verticale ?
Non so, forse sbaglio … ![]()
Ma non mi sembra che il percorso minimo sia necessariamente rettilineo visto in pianta, anche nel caso debba scavalcare una semplice parete ad altezza costante. ![]()
O forse non capisco cosa intendi ![]()
Ciao Emilio, sì.
E’ molto probabile che non abbia capito io allora.
Puoi postare un esempio veloce in cui il percorso minimo non sia, in pianta, rettilineo?
Dopo ci provo … ![]()
![]()
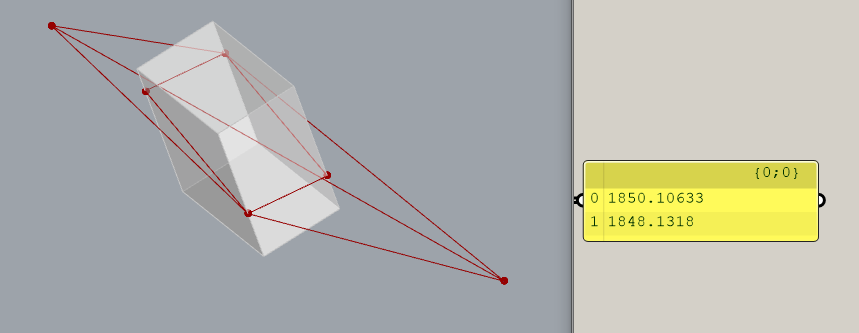
Esempio con parete da scavalcare ad altezza costante, non perpendicolare alla linea sfera-sfera e non equidistante dalle sfere …
Poi se c’entra qualcosa con quanto si diceva … e’ tutta un’altra faccenda. ![]()
![]()
fabio-3.gh (16,5 KB)
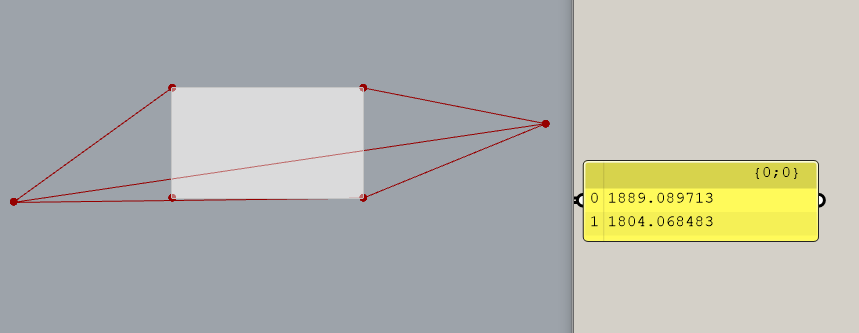
Ovviamente bisogna smanettare a mano sugli slider … ![]()
fabio-3 b.gh (18,0 KB)
I due segmenti devono incontrare il bordo superiore formando lo stesso angolo.
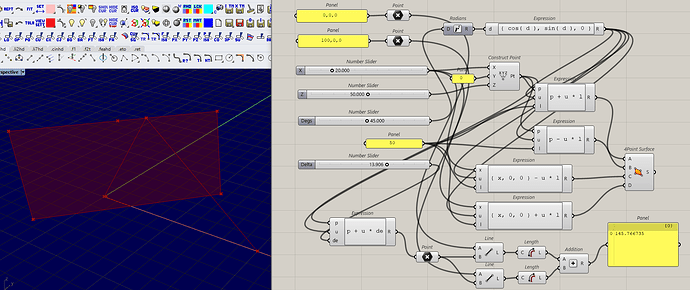
Il problema può essere risolto geometricamente pensando ad un foglio di carta con una piega:
la piega è il bordo superiore della parete da scavalcare, le due metà del foglio di carta sono due piani che passano ciascuno per uno dei due punti di inizio/fine.
Segni i due punti sul foglio di carta, raddrizzi il foglio, tracci una linea retta, ri-pieghi il foglio.
In pratica il foglio di carta è lo “spazio curvo” che si piega attorno al bordo superiore della parete, semplifichi lo “spazio curvo” in uno spazio planare, risolvi il problema, e riporti il risultato nello spazio curvo.
Tornando al post iniziale, non ho capito quanto complesso potrebbe diventare il problema, ma se ci sono n ostacoli e la situazione è complessa, io forse procederei con:
- dare uno spessore minimo ad ogni ostacolo, solido
- sottrazione booleana solida degli ostacoli al volume massimo percorribile, otteniamo un volume solido dove il percorso può esistere
- “tetraedrizzazione” del solito ottenuto
- propagazione iterativa da punto inizio a punto fine , shortest walk
- trovata così una polilinea grezza del percorso più breve (possibilmente)
- cleanup finale con algoritmo iterativo (kangaroo) per ottimizzare il percorso mantenendo attiva la collisione con gli ostacoli